Q. 小鳥居先生のご専門である「結び目理論」とはどんなものなのでしょうか？

結び目理論は、数学のなかのトポロジー（位相幾何学）の一分野です。トポロジーとは、「形を連続して変形させたものは同じものとみなす」というルールのもとでさまざまなものの形のもつ性質を数学的に研究する分野です。「コーヒーカップとドーナツは同じだ」という例が有名ですね。どちらも穴がひとつだけ空いている形なので、トポロジーでは同じ形とみなすことができます。

結び目理論を簡単に説明すると、輪っか状になった紐のさまざまな「絡まり方」を数式で書きあらわして分類したり、どんな性質があるのかを考えたりする研究です。

たとえば、ご祝儀袋についている「水引」のように紐が複雑に絡まっているところを想像してください。途中で切ったりすることなく、紐をたぐって動かしていくだけでシンプルな輪っかの状態に戻るものは数学的に絡まっていない状態といいます。反対に、いくら動かしてもどこかが引っかかって絶対に解けないものを数学的に絡まっている状態といいます。一見して複雑に絡まっている紐が、実際に数学的な意味で絡まっているかどうかを知りたい場合、見た目で判断することは困難です。そこで「結び目理論」の登場です。結び目理論では、複雑な紐の状態を数式に書き表します。それを解くことで紐がどのように絡まっているのか、あるいは絡まっていないのかを確かめることができるのです。

結び目理論で扱う代表的な結び目のひとつ、「三葉結び目」

現在、結び目たちを記述するための数式はたくさん知られていています。私が研究しているのはそのうちのいくつかの数式です。結び目が絡まっているかどうかは、数式を見ることで知ることができます。ですが結び目には無数のバリエーションがあって、すでに知られている数式を全部もってきても、すべての結び目を完全に記述することはできません。最終的には、すべての結び目を記述できるような統一的な理論を見つけ出すことをめざして、私たち結び目理論の研究者は研究を進めています。

Q. ものの形を扱う研究ということで、いろいろな分野に応用できそうですね。実際に他分野の研究者とも頻繁に交流されていると伺いました。

広島大学に来る前に理化学研究所の数理創造プログラム(iTHEMS)や革新知能統合研究センター (AIP)というところに所属していたのですが、そこはさまざまな分野の研究者が議論するなかで新しいものを生み出そうという組織でした。当時知り合った方々とは今も定期的に議論をしていますが、それだけではなく、他分野研究者との交流の際に障壁となるような文化の違いについても色々とアドバイスをいただけるとても貴重な存在となっています。最近ではACT-Xというグループに所属し、数学や情報の異なる分野の方達のお話を聞けて、とても勉強になっています。また、その他の異分野交流会にも積極的に参加するようにしています。専門分野の中だけだと研究者の数自体がどうしても限られてしまうのですが、他分野との交流を始めたことで一気にコミュニティが広がりました。数学とは違った別の世界を見せてもらえることが面白くて、いろいろな角度からの意見を聞く機会にもなっています。

交流を広げる一番の目的は、自分の視野を広げてくれるような異分野融合研究の相手を探すことです。とは言っても、自分が興味を持っていて役に立てる内容と、相手の研究者のニーズとが一致するのはそう簡単なことではありません。ですから最近は、自分の研究にしっかり軸足を置きつつ、一緒に研究できそうな相手をじっくり探すのが良いのかなと思っています。また、結び目理論という研究自体、他分野の方にはあまり知られていないと思いますので、交流会を通して知ってもらうのも大事なことですね。

現在、融合研究のお話が出ている分野としては生物学や工学などがあります。生物学に関しては、結び目理論を使ってDNAやタンパク質といった紐状の構造を分析する研究がすでにあり、工学では分子を紐状につないだポリマーの構造に結び目理論を応用する研究が進められています。具体的なことはお話できませんが、私もそうした方向でコラボレーションができないかと考えています。

Q. アウトリーチ（教育普及）活動にも力を入れていらっしゃるそうですね。

研究費をもらっている以上、研究成果を社会に知ってもらうことは研究者の義務ですし、こういう学問が有るということを知ってもらい、興味を持ってもらうきっかけとしてもアウトリーチ活動は大切だと思っています。とはいえ、数学の世界ではアウトリーチに力を入れている研究者は少数派かもしれません。トポロジーは図形や絵を沢山使いますから、一般の方に親しんでもらいやすいという点は有利ですね。

これまでに、理化学研究所の一般公開や高校への出張授業などで講演をさせていただきましたが、その時々の聴衆がどんな人々かを意識して、興味を持っていただけそうな具体例から始めるようにしています。高校生を対象に講演したときは、最初に水引や絡まった靴紐を見せて、「この紐は解けると思いますか？」とクイズを出しました。解ける場合の答え合わせは実際に解いてみればいいのですが、解けない場合、解けないことを証明する必要があります。さてどうしましょう……というところから数学の話に入っていきます。

高校生向けに行った講演会の様子

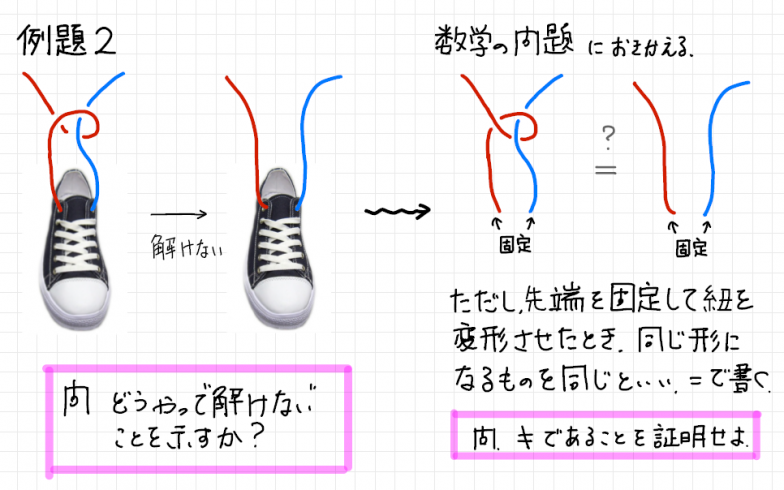
靴紐を導入にした高校生向けの講義スライド

アウトリーチ活動を通して気づきを得ることも多々あります。活動をはじめた頃は今ほどわかりやすく説明することができなかったのですが、ある親御さんが子どもさんに対して結び目を靴紐にたとえて教えてあげているのを見かけたことがありました。そうやって日常的なものに置き換えることで、厳密ではなくても多くの人にわかりやすく伝えることができるのだとそのときに気づいて、それから今の講演スタイルを確立することができました。

また、講演をすると必ず「どう社会の役に立つのか」ということを聞かれます。数学の基礎研究は理論を突き詰めるもので、基本的に社会の役に立つかどうかという視点は研究の中にありませんから、最初の頃はこうした質問を新鮮に感じました。すぐに何かの役に立つことだけが研究ではないということを知っていただきたいと思う一方で、世の中の役に立つような融合研究にも取り組んでみたいと思うようになったのは、アウトリーチ活動のおかげかもしれません。

Q. 小鳥居先生ご自身は、どうして数学研究者の道に進まれたのでしょうか？

小学生の頃から算数・数学が好きで、高校生のときに研究者になりたいと思うようになりました。大学に入ってすぐの頃は、やはり女性がとても少ないのでいろいろな面で苦労しましたね。大学院に進学するかどうかも迷ったのですが、やれるところまではやってみようということで、今に至ります。

トポロジーという分野に出会ったのも、大学の講義でのことでした。ものの形やその変化というと、一見、数学的に厳密に扱えなさそうに思えるのですが、トポロジーではそれを数学の言葉に落とし込んで議論できることに面白さを感じました。もともと絵を描いたり鑑賞したりすることも好きだったので、たくさん絵や図形が出てくるところに惹かれたというのもありますね。

Q. 最後に、今後の目標について教えてください。

専門分野の研究については、今興味を持っているテーマをひとつずつ着実に進めていきたいです。一方、融合研究も必ずやっていきたいと思っています。数学を研究しなければできないこと、そして数学を研究しているだけではできないことも両方やっていきたいですね。生物や工学、いろいろな分野にいろいろな「紐」がありますが、最終的にはそれらすべてを扱えるような統一的な理論を数学の世界で見つけたいと思っています。